对于债券来说，可以通过收益率计算出债券的价格进而得出盈亏，但过程较于繁琐，不利于投资决策，所以为了快速计算盈亏，提出久期的概念。

久期指的是收益率每变动1个基点，债券全价的百分比变动，用公式表示为：

在这里采用的是上下波动取均值的方法，其中y为收益率，V0为债券初始全价，V-为收益率下降y时对应的债券全价。

需要注意的时债券的价格和收益率变动是反向关系，但使用久期去估算，是有大前提的也就是债券的收益率与价格是线性关系。

但在实际上，债券价格P是收益率y的多项式函数（负次方）：

P=F(y)

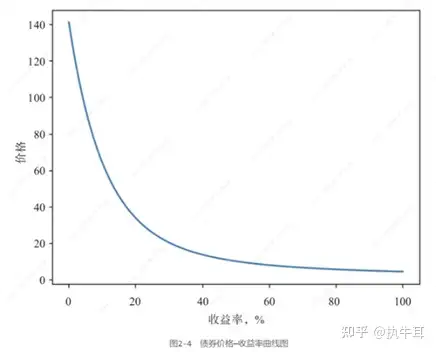
在微积分中，当收益率y在很小范围内变动的时候，可以用线性函数去近似多项式函数。其实，久期就起到了一个用直线求解曲线的近似值，当收益率变动越小，相应计算出来的误差就会越小。

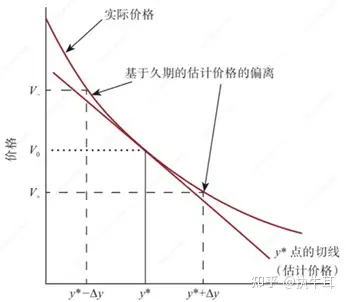
但当收益率变化较大的时候，所估计的价格误差也会比较大的，因此，又提出了凸性这一概念。

凸性式二次方函数，通过久期+凸性组合成一个二次方函数去近似表示真实的价格收益曲线。

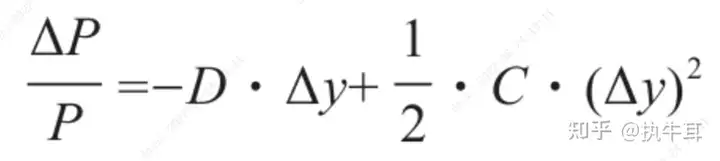
其中：D为久期、C为凸性。

其推导如下：

首先是债券价格和到期收益率的关系：

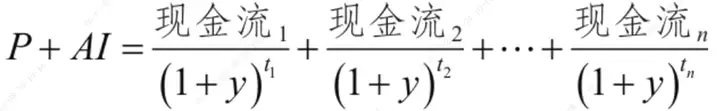
P为债券净值，AI为债券的应收利息，y为债券的到期收益率。

根据泰勒展开式：

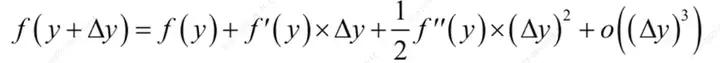
可以得到：

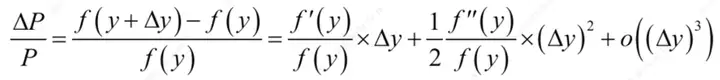
因此，债券价格的变化（应收利息不变，且应收利息占比较小，因此可以近似认为是净价的变化）

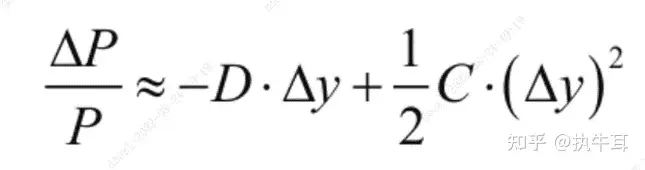
由此，我们也就知道了D是价格对收益率的一次导数，凸性C是价格对收益率的二次导数。

下面介绍久期如何计算：

麦考利久期

最终是为了衡量一只债券平均多长时间能够回收所有的现金流。但实际上没有什么用。

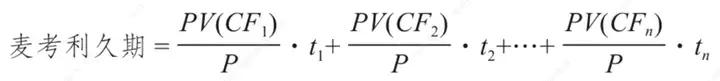
其中，ti是第i笔现金流的期限，PV(CFi)为第i笔现金流的贴现值，使用到期收益率进行贴现，P为债券的全价。

修正久期

 

其中，y为债券的到期收益率，f为每年的付息次数。

它表示债券价格百分比变动对收益率变动的相对值，目前中债登提供的估值数据都是估值修正久期。

修正久期的一个前提假设是：其预期的未来现金流不会随着收益率变化而变化，对于不含权债券是没有问题的，但对于含权债券，包括ABS,这个假设并不成立，这时候就需要用到有效久期。

有效久期

和久期概念一致，表示收益率变动对债券价格百分比变动的敏感性。

 

对于收益率的变动不但影响未来现金流的贴现值，还会影响现金流本身（时间和金额），在这种情况下，最常用也最精确的是使用简单的蒙特卡洛模拟，模拟收益率变动下的各种不同利率路径、估计在不同利率路径下的债券的现金流、现金流贴现得出债券价格、通过久期的公式进行计算。

基点价值

指每百元面值的债券，当收益率变动1个基点时，债券的价格的绝对值的变动，有时被称为DV01.

附个例题：