金融投资组合（Python 金融: 建立A股最优投资组合）

在前文作者尝试了用 TuShare API 抓去A股的历史价格K线：

多多教Python：Python 金融: TuShare API 获取股票数据 (1)13 赞同 · 5 评论文章

现在我们来根据我们感兴趣的A股票子，获取历史价格K线之后，纯粹的根据历史价格走势来配置仓位。配置仓位的方法是根据投资组合管理理论里的 最优投资组合:

投资组合理论_百度百科baike.baidu.com/item/%E6%8A%95%E8%B5%84%E7%BB%84%E5%90%88%E7%90%86%E8%AE%BA/6602455?fr=aladdin

这里要介绍的是两种最优解：一种是 夏普比率 Sharpe Ratio 最优化，可以理解为风险补偿后的回报率最大的投资组合；另外一种是 波动率 Volatility 最优化，也就是波动率最小，风险最低的投资组合。

好了，现在我们开始进入教程，在这之前需要完成下列需求：

Mac OS (Windows, Linux 步骤相似，但是不完全一样)
安装了 Python 3.0 版本以上,Anaconda
阅读了多多教Python：Python 金融: TuShare API 获取股票数据 (1) ，多多教Python：Python 基本功: 11. 初学 Pandas 库

最优投资组合

我们知道风险和收益是成正比的，较大的风险会获得较大的预期回报，而较小的风险则会有较小的预期回报。在一个投资组合中，我们往里面塞了不同的股票，给予了不同的权重，形成了一个投资组合，而这个投资组合则有一个属于自己的风险和预期回报率。

一个投资组合所持有的风险，不一定能带来最大化的收益。换句话说，你的投资组合也许承担了较大的风险，却只能获得较小的预期收益。原因可能在于你过大的权重了一只表现较差的股票，或者投资组合里的股票数量少，并且每一只股票都自带非常大的风险。

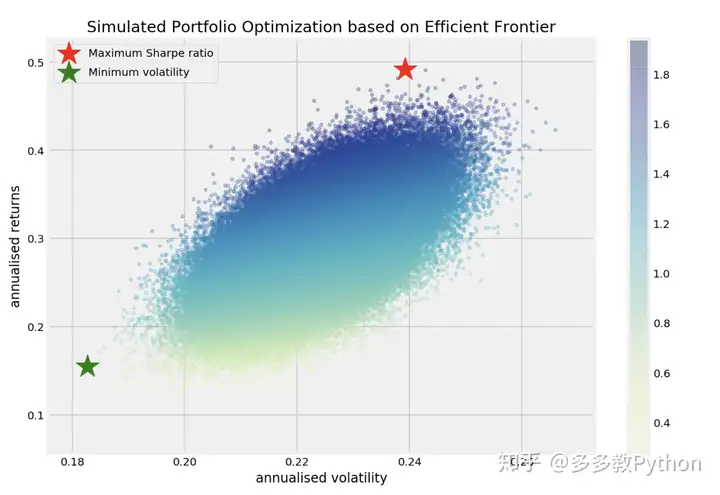
最优投资组合是建立在一条叫 有效边际 Efficient Frontier 之上的，例如下图：

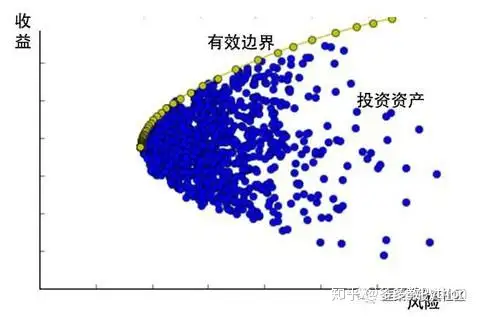
我们可以看到，在这条有效边界上的，都是风险收益比最高的投资组合，而在内部的蓝点都不是最优化的组合资产。你可以调整你的仓位权重来让你的投资组合站在有效边际上，而这篇 Python 教程就告诉你一个简单的优化方法帮你免去不必要的风险。

股票筛选

在这篇教程中，我选择了A股中超高市值，超高流动性，白马蓝筹扛把子级别的50支股票。不过这不是作者的实盘仓位。

我们这里先偷窥一下结果，下图展示了作者写完教程之后生成的 夏普比率 Sharpe Ratio 最优的投资组合：

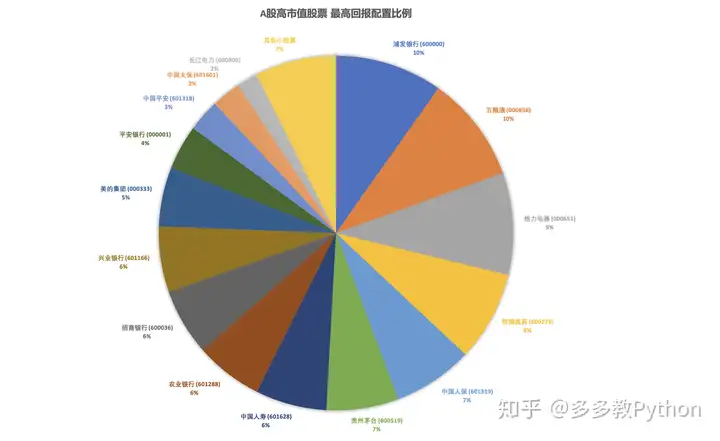
其中票子有：

浦发银行，五粮液，格力电器，恒瑞医药，中国人保，贵州茅台，中国人寿，农业银行，招商银行，兴业银行，美的集团，平安银行，中国平安，中国太保，长江电力。。。

这里我们可以看到浦发银行和五粮液是最大的权重，各10%，随后是格力电器 9%，恒瑞医药 8%，中国人保和贵州茅台各7%。

下面我们先通过 TuShare API 来获取这些股票的历史价格：

In [1]: 
import tushare as ts
import pandas as pd  
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.optimize as sco

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

In [2]:
stock_codes = ['601857', '601628', '601398', '600036', '600028', '601288', '601998', 
               '601601', '601319', '601166', '601138', '601088', '600900', '600276', 
               '600000', '002415', '000333', '000001', '000002', '600019', '000651', 
               '000858', '601318', '600519', '600030']
num_stocks = len(stock_codes)
stock_daily_quotes = {}

In [3]:
import time
for code in stock_codes:
    print(code)
    df = ts.get_k_data(code=code, start='2015-10-01', end='2019-10-01')
    df = df.set_index(['date'])
    df[code] = df['close']
    stock_daily_quotes[code] = df[code]
    time.sleep(1)

In [1]: 这里我用的是 Jupyter Notebook, 还没有安装的小伙伴可以从多多教Python：Python 基本功: 1. Hello world 看起来了。上来先把需要的模块导入，包括 TuShare API, Pandas, Numpy, Matplotlib, Seaborn 和 Scipy。我在教程里讲过了前三个，有兴趣的小伙伴可以去分别了解一下:

多多教Python：Python 基本功: 11. 初学 Pandas 库31 赞同 · 2 评论文章

多多教Python：Python 基本功: 12. 高纬运算的救星 Numpy3 赞同 · 1 评论文章

In [2]: 随后是在一个列表里写入了我准备纳入投资组合的25个股票代码，票子的名字我就不一一对应了。
In [3]: 调用 tushare API 获取股票历史K线，时间从 2015年10月1号到2019年10月1号。作者选择的25个票子在这4年都有交易，没有ST，合并，拆分等需要特殊处理的，所以获取之后直接按照 Close 当日结束价格为准。每获取一个票子停顿一秒钟，不要去阻塞 tushare 的端口。

数据检查

在通过 API 获取数据之后，我们对获得的股票数据通过 Pandas 做一下简单的检查，看看有没有什么毛病：

In [4]: all_df = pd.concat([value for _, value in stock_daily_quotes.items()], axis=1)

In [5]: all_df.head()
Out [5]:
601857	601628	601398	600036	600028	601288	601998	601601	601319	601166	...	002415	000333	000001	000002	600019	000651	000858	601318	600519	600030
2015-10-08	8.128	24.741	3.809	15.957	4.183	2.650	5.366	20.973	NaN	13.164	...	14.385	16.538	8.518	11.676	5.251	14.817	NaN	28.759	187.805	13.236
2015-10-09	8.205	25.228	3.861	16.164	4.303	2.659	5.393	22.078	NaN	13.307	...	14.355	16.532	8.677	11.819	5.278	14.844	NaN	29.677	187.263	13.449
2015-10-12	8.446	25.696	3.922	16.371	4.406	2.710	5.545	22.484	NaN	13.520	...	15.168	17.257	8.940	12.042	5.442	15.407	NaN	30.577	188.347	14.248
2015-10-13	8.359	25.610	3.870	16.254	4.354	2.693	5.545	22.511	NaN	13.404	...	15.219	17.032	8.860	12.033	5.406	15.302	NaN	30.165	188.965	14.164
2015-10-14	8.408	25.295	3.852	16.065	4.337	2.667	5.581	21.986	NaN	13.369	...	14.732	16.452	8.741	11.863	5.351	15.046	NaN	29.677	188.100	14.164
5 rows × 25 columns

In [6]: all_df = all_df.dropna() # 非生产代码，需要做更加精细的处理

[4]: 因为我们下载的每一支股票的数据都在各自的 DataFrame里，通过 Pandas 的 Concat 方法把他们合并到一个 DataFrame 数据框里。
[5]: 现在我们来检视一下整合完毕的 DataFrame。我们发现 Index 索引是日期，从10月8号开始，因为10月1号到7号是国庆节休市。而其中有一列都是 NaN 数据，说明有的股票代码可能当天没有交易。
[6]: 这里我们需要对数据进行清洗。作者简单的把所有包含 NaN 的数据列和行给删除了。我也在后面标注了这不是生产代码，生产代码需要更加精细的对缺失数据进行处理。

有兴趣的小伙伴还可以把票子价格 Plot 出来，这里作者简单的画出了25支股票的价格走势图：

和25支股票的2015-2019日回报率：

代码作者就不展示出来了，读者根据自己的需求可以画出不同的图，当然也可以拷贝数据到 Excel 去画，参考：多多教Python：Python 基本功: 11. 初学 Pandas 库。

定义优化方程

接下来的几段代码，一部分作者也是从网上找到整合起来的，有自己的优化部分，所以如果原作者看到了可以留言给我我来给你加引用。

获得了股票价格数据之后，我们根据其价格走势和回报波动率来优化其权重。做过优化的小伙伴知道，做优化之前首先定义优化目的，和优化方法：

In [7]:
def portfolio_annualised_performance(weights, mean_returns, cov_matrix):
    returns = np.sum(mean_returns*weights ) *252
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights))) * np.sqrt(252)
    return std, returns

In [8]:
def random_portfolios(num_portfolios, mean_returns, cov_matrix, risk_free_rate):
    results = np.zeros((num_stocks,num_portfolios))
    weights_record = []
    for i in range(num_portfolios):
        weights = np.random.random(num_stocks)
        weights /= np.sum(weights)
        weights_record.append(weights)
        portfolio_std_dev, portfolio_return = portfolio_annualised_performance(weights, mean_returns, cov_matrix)
        results[0,i] = portfolio_std_dev #波动率目标
        results[1,i] = portfolio_return
        results[2,i] = (portfolio_return - risk_free_rate) / portfolio_std_dev # 夏普比率目标
    return results, weights_record

这里优化目标的有两个，就像教程一开始所介绍的，夏普比率 Sharpe Ratio 和 波动率 Volatility, 具体位置我在代码里用中文标注了。优化方法采用了随机采样随后比较结果，也就是随机生成25支股票的权重，随后比较随机生成的结果，最后获取结果最好的。

参数设置

定义了优化目标和优化方程之后，我们需要对其输入我们优化的参数：

In[9]:
returns = all_df.pct_change()
mean_returns = returns.mean()
cov_matrix = returns.cov()
num_portfolios = int(25000 / 2.5 * num_stocks)
risk_free_rate = 0.027

这里需要优化的参数包括了:

returns: 每只股票的日回报百分比。
mean_returns: 每只股票的日回报百分比平均。
cov_matrix: 每只股票的日回报百分比协方差。
num_portfolios: 想要生成多少个随机投资组合，数字越大越接近真实的最优解，但是也会消耗CPU资源。
risk_free_rate: 无风险利息，我取的是余额宝利率: 2.7%

开干！

下面一段代码做的就是生成一个随机投资组合，然后计算投资组合的回报率，波动率等，然后排序，找到最优的一个投资组合，并且展现出来：

In [10]:
def display_simulated_ef_with_random(mean_returns, cov_matrix, num_portfolios, risk_free_rate):
    results, weights = random_portfolios(num_portfolios,mean_returns, cov_matrix, risk_free_rate)
    
    max_sharpe_idx = np.argmax(results[2])
    sdp, rp = results[0,max_sharpe_idx], results[1,max_sharpe_idx]
    max_sharpe_allocation = pd.DataFrame(weights[max_sharpe_idx],index=all_df.columns,columns=['allocation'])
    max_sharpe_allocation.allocation = [round(i*100,2)for i in max_sharpe_allocation.allocation]
    max_sharpe_allocation = max_sharpe_allocation.T
    
    min_vol_idx = np.argmin(results[0])
    sdp_min, rp_min = results[0,min_vol_idx], results[1,min_vol_idx]
    min_vol_allocation = pd.DataFrame(weights[min_vol_idx],index=all_df.columns,columns=['allocation'])
    min_vol_allocation.allocation = [round(i*100,2)for i in min_vol_allocation.allocation]
    min_vol_allocation = min_vol_allocation.T
    
    print("-"*80)
    print("Maximum Sharpe Ratio Portfolio Allocation\n")
    print("Annualised Return:", round(rp,2))
    print("Annualised Volatility:", round(sdp,2))
    print("\n")
    print(max_sharpe_allocation)
    print("-"*80)
    print("Minimum Volatility Portfolio Allocation\n")
    print("Annualised Return:", round(rp_min,2))
    print("Annualised Volatility:", round(sdp_min,2))
    print("\n")
    print(min_vol_allocation)
    
    plt.figure(figsize=(10, 7))
    plt.scatter(results[0,:],results[1,:],c=results[2,:],cmap='YlGnBu', marker='o', s=10, alpha=0.3)
    plt.colorbar()
    plt.scatter(sdp,rp,marker='*',color='r',s=500, label='Maximum Sharpe ratio')
    plt.scatter(sdp_min,rp_min,marker='*',color='g',s=500, label='Minimum volatility')
    plt.title('Simulated Portfolio Optimization based on Efficient Frontier')
    plt.xlabel('annualised volatility')
    plt.ylabel('annualised returns')
    plt.legend(labelspacing=0.8)
    
    return max_sharpe_allocation, min_vol_allocation

In [11]:
max_sharpe_alloc, min_vol_alloc = display_simulated_ef_with_random(mean_returns, cov_matrix, num_portfolios, risk_free_rate)

作者的机器是 iMac 2018 顶配，但是这个脚本计算用的是单核，所以还是比较慢，每一次跑需要15分钟左右，小伙伴可以参考：

多多教Python：Python 基本功: 14. 多核并行计算511 赞同 · 29 评论文章

更新一下 In [10] 这段代码，做平行计算，应该可以提速几倍。

下面展示一下我跑出来的结果：

--------------------------------------------------------------------------------
Maximum Sharpe Ratio Portfolio Allocation

Annualised Return: 0.49
Annualised Volatility: 0.24


            601857  601628  601398  600036  600028  601288  601998  601601  \
allocation    1.78    5.46    0.99    0.73    6.55    2.06    3.41    1.74   

            601319  601166  ...  002415  000333  000001  000002  600019  \
allocation    8.29    7.24  ...     4.8    1.03    7.24    1.35    1.36   

            000651  000858  601318  600519  600030  
allocation    3.46    9.32    2.89   11.35    6.33  

[1 rows x 25 columns]
--------------------------------------------------------------------------------
Minimum Volatility Portfolio Allocation

Annualised Return: 0.15
Annualised Volatility: 0.18


            601857  601628  601398  600036  600028  601288  601998  601601  \
allocation   11.47    5.62    2.81    2.19    8.05    7.07    8.89    1.49   

            601319  601166  ...  002415  000333  000001  000002  600019  \
allocation    3.06    0.11  ...    0.24    0.41    0.78    7.88     4.2   

            000651  000858  601318  600519  600030  
allocation    5.43    1.92    1.91    1.95    0.46  

[1 rows x 25 columns]

下图也是自动生成的，两个最优投资组合已经用星号标好了：

下面我们来看看 夏普比率最优 组合里面的票子权重是什么样的：

In [12]: print(max_sharpe_alloc)
            601857  601628  601398  600036  600028  601288  601998  601601  \
allocation    1.78    5.46    0.99    0.73    6.55    2.06    3.41    1.74   

            601319  601166  ...  002415  000333  000001  000002  600019  \
allocation    8.29    7.24  ...     4.8    1.03    7.24    1.35    1.36   

            000651  000858  601318  600519  600030  
allocation    3.46    9.32    2.89   11.35    6.33  

[1 rows x 25 columns]

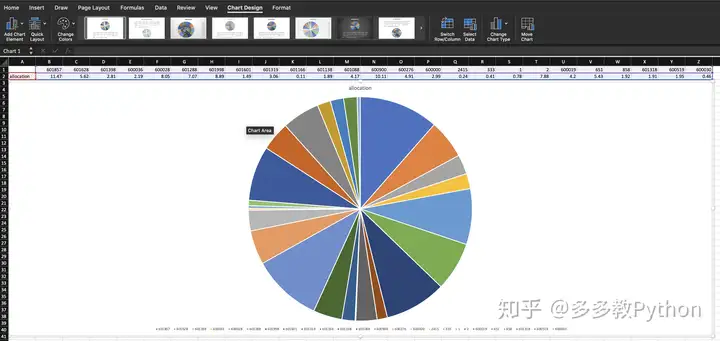
我们也可以把 max_sharpe_alloc 和 min_vol_alloc 两个 Pandas DataFrame 的数据拷贝到 Excel 去查看：

小结：

小伙伴不妨可以多试试筛选出来不同的票子，来跑这篇教程来做一个投资组合优化，也可以拿你现在拿着的A股票子跑一下。当然这里要注意的是：

拿到股票数据之后要做仔细的数据清洗，保证优化的是正确的每日交易数据，这点很重要。
这篇教程的代码不是生产代码，如果要用来做实盘需要更加专业化的调整。

在你根据自己的需求生成好了最优投资组合之后，你可以和你已有的实盘仓位配置比较一下，看看是否在今后的走势中达到了实盘的效果。这里的最优投资组合是根据股票的历史数据，并且是理论上的最优选，不代表生成出来的一定是在今后的盘面上最优选。

不过作者还是强烈建议使用这样的 Python 工具来 DIY 你的投资组合，更加理性科学的安排你的仓位，在2020年打败大盘获利。